R là tập hợp số gì ví dụ
Trong toán học có rất nhiều ký hiệu tập số khác nhau, mỗi ký hiệu đại diện cho một tập số nhất định. Khi tìm hiểu các tập số trong toán học, nhiều người thắc mắc không biết R là tập số gì và nó có tính chất như thế nào?
Cho những ai chưa biết R là tập hợp số gì thì R là ký hiệu của tập hợp số thực, một tập hợp bao gồm tất cả các số được biểu diễn trên trục số thực. Điều này có nghĩa là nó bao gồm tất cả các loại số mà chúng ta thường gặp trong toán học, từ các số nguyên như -3, 0, và 5, đến các số hữu tỉ (những số có thể được biểu diễn dưới dạng phân số của hai số nguyên).

Bên cạnh đó, tập hợp số thực còn chứa các số vô tỉ (những số không thể biểu diễn dưới dạng phân số và có phần thập phân kéo dài vô hạn mà không lặp lại). Các số thập phân như 3.14, -2.718, và 0.333 cũng nằm trong tập hợp số thực.
Nói một cách tổng quát, tập hợp R bao gồm tất cả các số có thể được biểu diễn dưới dạng một điểm trên trục số, không kể chúng là số nguyên, hữu tỉ hay vô tỉ.
Ví dụ về tập R:
- Số nguyên: -2, 1, 8,...
- Số hữu tỉ: ½, ⅝ ,....
- Số thập phân: 0.33, -1.22,...
- Số 0
R là gì trong hình học?
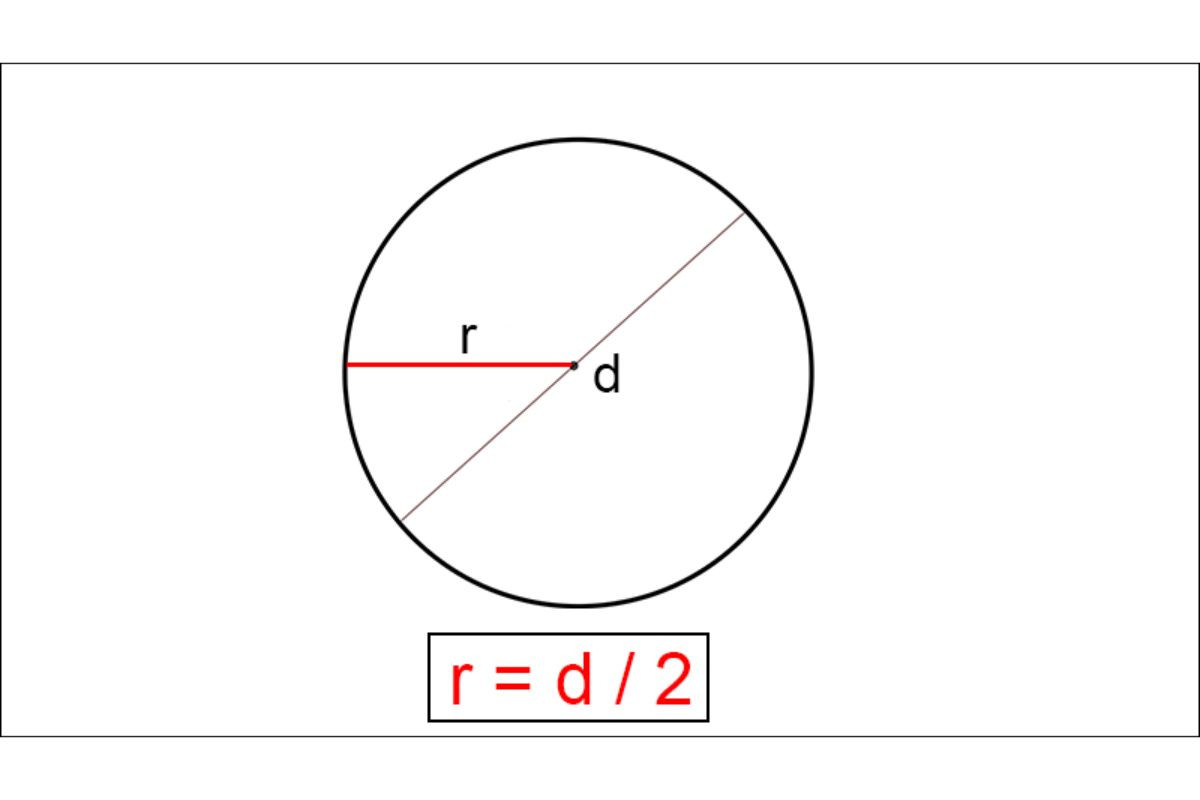
Trong đại số, R là tập hợp số thực, vậy trong hình học, R là tập hợp số gì? Thực tế, R trong hình học không phải là một tập hợp số mà là ký hiệu bán kính của đường tròn. R là kích thước từ tâm đường tròn đến một điểm bất kỳ trên đường tròn đó. Bán kính R của đường tròn có kích thước bằng ½ đường kính của hình tròn.
Tập hợp R có số 0 không?
Không chỉ tìm hiểu R là tập hợp số gì, tập hợp R có số 0 không cũng là vấn đề được nhiều người quan tâm. Theo quy ước toán học, tập hợp R bao gồm số 0 bởi nó bao gồm tất cả các số có thể được biểu diễn trên trục số như số nguyên, số hữu tỉ, số vô tỉ và số thập phân. Trong đó, số 0 là số nguyên và cũng là số thực nên chắc chắn nó sẽ thuộc tập R.

Tính chất của tập số thực R
Để vận dụng tập số R vào việc giải quyết các phép toán và bài toán có liên quan, bạn cần biết R là tập hợp số gì và nắm rõ các tính chất của tập số thực R. Tập số thực R có các tính chất sau:
- Tập hợp R có tính liên tục, nghĩa là giữa bất kỳ hai số thực nào cũng có một số thực khác.
- Các số thực trong tập R có thể sắp xếp theo thứ tự từ nhỏ đến lớn và ngược lại.
- Phép cộng hai số thực bất kỳ cho ra kết quả là một số thực.
- Phép trừ hai số thực bất kỳ cũng cho ra kết quả là một số thực.
- Phép nhân hai số thực bất kỳ cho ra kết quả là một số thực.
- Phép chia hai số thực bất kỳ (trừ số 0) cũng cho ra kết quả là một số thực.
- Số phần tử trong tập hợp R là vô hạn
- Không có bất kỳ số thực nào lớn nhất và cũng không có bất kỳ số thực nào nhỏ nhất.
Những tính chất này làm cho tập hợp R trở thành một nền tảng quan trọng cho nhiều lĩnh vực toán học, bao gồm giải tích, đại số, và hình học.
Các tập con của tập hợp số R
Sau khi biết R là tập hợp số gì, bạn cũng sẽ nắm được các tập hợp con của tập hợp R cũng như mối quan hệ giữa tập số thực R với các tập hợp số khác trong toán học. Cụ thể:
Tập hợp số tự nhiên N
Trong toán học, N là tập hợp số tự nhiên, trong đó tập hợp tất cả các số tự nhiên bao gồm cả số 0 được ký hiệu là N và tập hợp các số tự nhiên khác 0 được ký hiệu là N*. Vì mọi số tự nhiên đều là số thực và có thể biểu diễn trên trục số, do đó khi đã nắm rõ R là tập hợp số gì, bạn sẽ biết được N là tập hợp con của R, ký hiệu N ⊂ R.
Tập số nguyên Z
Trong toán học, Z là ký hiệu của tập hợp số nguyên, trong đó, số nguyên âm được ký hiệu là Z- và số nguyên dương được ký hiệu là Z+. Vì số nguyên cũng là số thực, do đó, khi đã biết tập hợp R là tập hợp gì, Z là tập hợp gì, bạn sẽ biết được Z cũng là tập hợp con của tập R, ký hiệu Z ⊂ R.
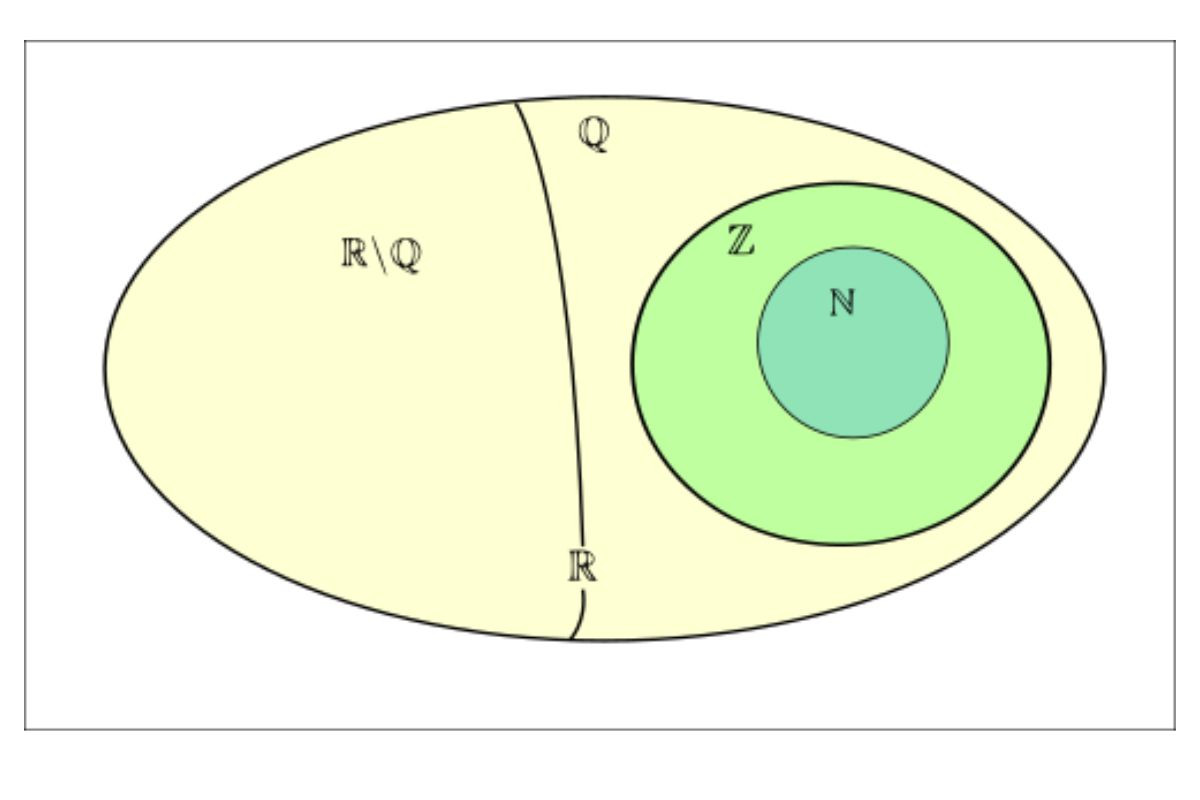
Tập hợp số hữu tỉ Q
Q là ký hiệu của tập hợp số hữu tỉ trong toán học. Số hữu tỉ là những số có thể biểu diễn dưới dạng phân số, trong đó mẫu số khác 0. Vì tập số thực R bao gồm các số hữu tỉ nên Q cũng là tập hợp con của R. Trên trục số thực, các số hữu tỉ nằm ở các vị trí tương ứng với các phân số của các số nguyên. Do đó, mỗi phần tử của Q cũng là một phần tử của R.
Ký hiệu: Q ⊂ R
Tóm lại:
- Tập hợp số tự nhiên (N) là tập hợp con của tập hợp số thực R.
- Tập hợp số nguyên (Z) là tập hợp con của tập hợp số thực R.
- Tập hợp số hữu tỉ Q là tập hợp con của tập hợp số thực R.
Ý nghĩa của tập R trong toán học
Tập hợp R trong toán học đóng vai trò rất quan trọng vì nó là nền tảng cho rất nhiều dạng bài tập toán khác nhau. Vì vậy, việc hiểu rõ R là tập hợp số gì và tính chất của tập hợp R là rất cần thiết. Dưới đây là ý nghĩa của tập hợp R mà bạn có thể tham khảo:

- Vi phân: Số thực được sử dụng để mô tả độ dốc của đường cong tại một điểm. Đạo hàm của một hàm số thực xác định tốc độ thay đổi tức thời của hàm số đó.
- Tích phân: Số thực được sử dụng để tính toán diện tích dưới đường cong hay nói cách khác là để tính toán tích lũy của các lượng liên tục.
- Giải phương trình và bất phương trình: Nghiên cứu nghiệm của các phương trình và bất phương trình trong tập số thực. Ví dụ, nghiệm của phương trình bậc hai có thể là một số thực.
- Hàm số: Các hàm số thực là cơ sở để mô tả mối quan hệ giữa các biến. Ví dụ, hàm số bậc nhất, hàm số bậc hai, hàm số mũ đều liên quan đến số thực.
- Biến ngẫu nhiên: Biến ngẫu nhiên có thể nhận các giá trị là các số thực. Ví dụ, phân phối chuẩn được mô tả bằng các số thực.
- Ước lượng và kiểm định giả thuyết: Sử dụng các số thực để tính toán các tham số mẫu, khoảng tin cậy, và giá trị p trong kiểm định giả thuyết.
Ngoài ra tập số thực R còn có tính ứng dụng trong khoa học, kỹ thuật. Chẳng hạn như trong vật lý, số thực được sử dụng để mô tả các đại lượng vật lý như tốc độ, gia tốc, lực, năng lượng. Trong tài chính, số thực được dùng để mô tả giá trị tiền tệ, lãi suất, và các chỉ số tài chính khác.
Một số dạng toán về tập hợp số R
Để giải quyết các bài toán liên quan đến tập hợp R, bạn cần phải biết R là tập hợp số gì, tập hợp R có số 0 không, đồng thời phải nắm rõ các tính chất cơ bản của tập hợp R trong toán học. Dưới đây là những dạng toán liên quan đến tập hợp R mà bạn có thể tham khảo:
Dạng 1: Các phép toán với tập số thực R:

Bài tập về các phép toán với tập số thực R bao gồm các phép cộng, trừ, nhân, chia. Và tất nhiên, để thực hiện các phép toán này, bạn cần biết R là tập hợp số gì và tính chất của tập hợp R. Dưới đây là các ví dụ về phép toán với tập số thực R:
- Tính giá trị của biểu thức: 3.7 + 5.2 - 8.9
- Tính giá trị biểu thức -4.5 + 8.3 = 3.8
- Tính giá trị biểu thức 4.2 x 3 = 12.6
- Tính giá trị biểu thức -8.4 : 2 = -4.1
Dạng 2: Giải phương trình:
Sau khi biết R là tập hợp số gì, bạn có thể áp dụng tính chất của tập hợp R để giải phương trình tìm x. Dưới đây là các ví dụ về giải phương trình với tập số thực R:
- Giải phương trình: 2x + 5 = 11
=> 2x = 11 - 5 = 6
=> x = 6 : 2
=> x = 3
- Giải phương trình 3.5x - 7 = 0
=> 3.5x = 0+7 = 7
=> x = 7 : 3.5
=> x = 2
Dạng 3: Giải bất phương trình:
Bạn cũng có thể ứng dụng tính chất của tập hợp R vào giải bất phương trình trong toán học. Dưới đây là các ví dụ về giải bất phương trình với tập số thực R:
- Giải bất phương trình: 2x - 3 > 5
=> 2x > 5+ 3
=> 2x > 8
=> x > 4
- Giải bất phương trình: -4x + 7 < 3
=> -4x < 3 - 7
=> -4x < -4
=> x > 1
Dạng 4: So sánh 2 số thực trong tập hợp R:
Dạng bài tập so sánh 2 số thực yêu cầu bạn phải nắm rõ R là tập hợp số gì và các tính chất của tập R. Dưới đây là các ví dụ về dạng toán so sánh 2 số thực trong tập hợp số R:
- So sánh: 5.6 và 8.9 => 5.6 < 8.9
- So sánh: 0 và -0.1 => 0 > -0.1
Nắm rõ R là tập hợp số gì và những tính chất cơ bản của tập hợp R trong toán học không chỉ giúp bạn hiểu rõ về cấu trúc và tính chất của các số thực mà còn là nền tảng để giải quyết các bài toán liên quan. Bên cạnh đó, việc hiểu rõ các tập hợp con của R và ý nghĩa của tập số thực R cũng giúp bạn tránh được những sai sót nhỏ khi thực hiện các phép toán và giải bài tập liên quan đến số thực.