Phương trình tính đường cao trong tam giác - Cách tính đường cao trong tam giác

Bạn muốn tính đường cao trong tam giác nhưng không nhớ công thức? Hãy đọc bài viết này để tìm hiểu cách tính đường cao trong tam giác.

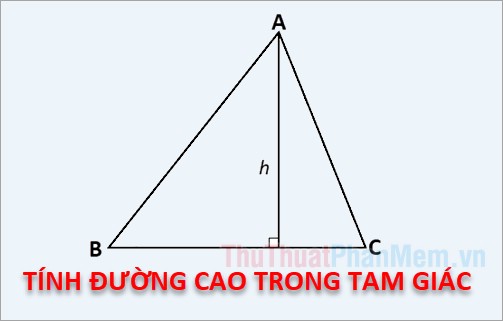
Dưới đây là công thức tính đường cao trong tam giác, mời bạn đọc theo dõi.

Đường cao trong tam giác là gì?

Đường cao của tam giác là đoạn thẳng kẻ từ một đỉnh vuông góc với cạnh đối diện. Độ dài của đường cao chính là khoảng cách từ đỉnh đến đáy.

Công thức tính đường cao trong tam giác

Để tính đường cao trong tam giác, bạn có thể sử dụng công thức Heron như sau:

ha=2√p(p−a)(p−b)(p−c)aha=2p(p−a)(p−b)(p−c)a

Với các giá trị a, b, c là độ dài các cạnh tam giác và ha là đường cao từ đỉnh A xuống cạnh BC, ta có p là nửa chu vi tam giác:

p=(a+b+c)2p=(a+b+c)2

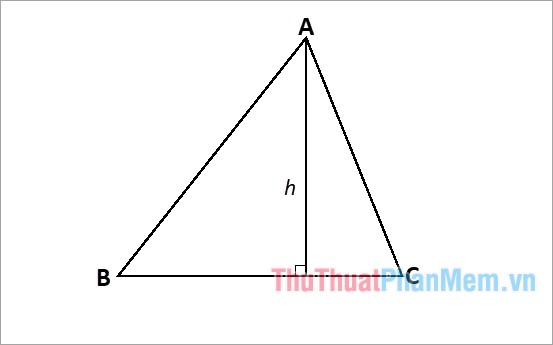
Công thức tính đường cao trong tam giác đều

Cho tam giác đều ABC có độ dài cạnh bằng a như sau:

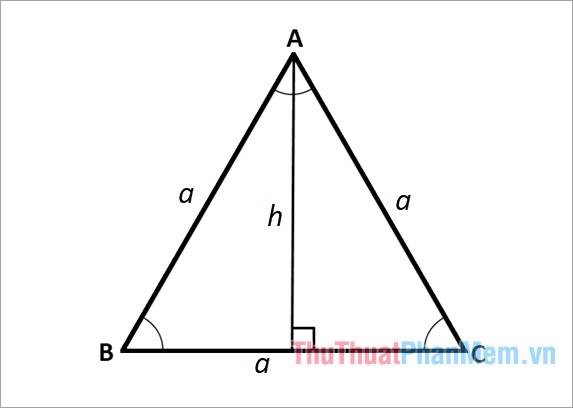
Đường cao tính bằng: h=a√32h=a32

Trong trường hợp này: h là chiều cao của tam giác đều và a được dùng để đo độ dài cạnh của tam giác đều.

Công thức tính đường cao trong tam giác vuông

Giả sử chúng ta có tam giác vuông ABC vuông tại đỉnh A như dưới đây:

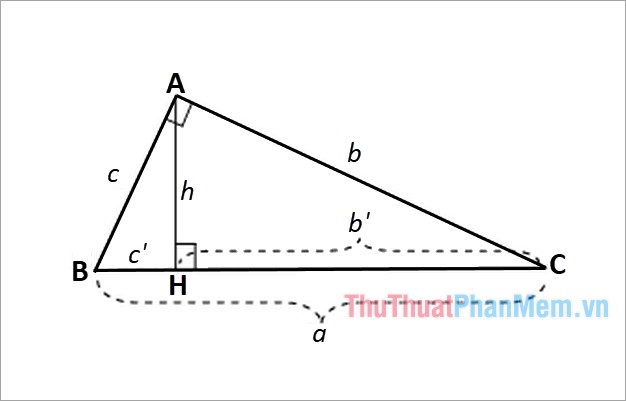
Công thức tính cạnh và đường cao trong tam giác vuông:

1. a2=b2+c2a2=b2+c2

2. b2=a.b′b2=a.b′ và c2=a.c′c2=a.c′

3. ah = bc

4. h2=b′.c′h2=b′.c′

5. 1h2=1b2+1span>c21h2=1b2+1c2

Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;

b’ là đường chiếu của cạnh b trên cạnh huyền; c’ là đường chiếu của cạnh c trên cạnh huyền;

h là độ dài đoạn thẳng từ đỉnh A vuông góc với cạnh BC trong tam giác vuông ABC.

Do đó, bạn có thể áp dụng các công thức tính cạnh và đường cao trong tam giác vuông để giải quyết các bài toán.

Công thức tính đường cao trong tam giác cân

Xét tam giác ABC cân tại đỉnh A, đường cao AH được kẻ từ đỉnh A vuông góc với cạnh BC như sau:

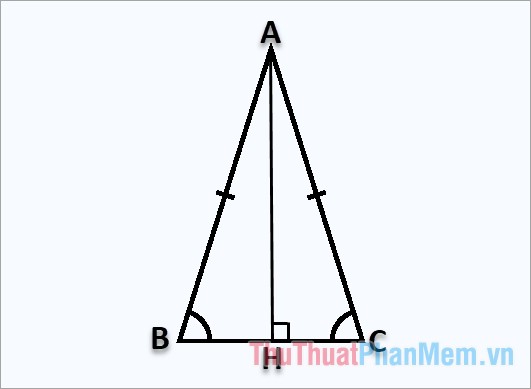
Một phép tính phức tạp nhưng cân bằng và hợp lý, chúng ta có thể suy luận ra rằng A bằng B nhân với chính nó.

Dễ dàng nhận thấy rằng khi A bằng B bình phương trừ đi B nhân với chính nó, chúng ta thu được một kết quả đáng chú ý.

Khi áp dụng vào bài toán tính đường cao trong tam giác, ta có thể giải quyết những yếu tố chưa biết một cách hiệu quả, từ đó tìm ra đáp án một cách nhanh chóng và chính xác.